Semejanza
La aplicación de la proporcionalidad a la geometría conduce al concepto de semejanza entre figuras que se utiliza en la construcción de planos, mapas y maquetas, necesarios para poder representar la realidad en un tamaño manejable, interpretarla y planificar proyectos.
Esta secuencia contiene:
-
15 actividades
-
81 recursos
-
Idioma:
- Castellano
-
Formato:
Interactivo
Secuencia didáctica
-
Objetivos didácticos Conocer el teorema de Tales, comprobarlo y utilizarlo para resolver problemas de geometría. Reconocer cuándo dos triángulos son semejantes. Conocer los criterios de semejanza de triángulos. [...]
-
7. Semejanza 1. Teorema de Tales Teorema de Tales: Los segmentos determinados en dos rectas secantes al ser cortadas por rectas paralelas son proporcionales. [...]
-
La aplicación de la proporcionalidad a la geometría conduce al concepto de semejanza entre figuras que se utiliza en la construcción de planos, mapas y maquetas, necesarios para poder representar la realidad en un tamaño manejable, interpretar...
-
Observa la figura siguiente. En ella, dos rectas secantes, r y s, son cortadas por varias rectas paralelas entre sí, determinando los puntos A, B y C en la recta s y los puntos A', B' y C' en la recta r. [...]
-
Dos triángulos son semejantes si los lados correspondientes son proporcionales y los ángulos correspondientes son iguales. [...]
-
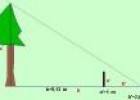
La semejanza de triángulos se aplica en la vida real para calcular distan cias o alturas de objetos. Ejemplo 1 Aplica la semejanza de triángulos para medir la altura de un árbol. [...]
-
Vamos a obtener los teoremas del cateto, de Pitágoras y de la altura utilizando la semejanza. [...]
-
Dos figuras son semejantes si tienen la misma forma, aunque su tamaño sea diferente. 5.1 Polígonos semejantes Los dos polígonos de la derecha son figuras semejantes. [...]
-
6.1 Método de proyección Utilizamos este método para construir un polígono semejante a otro: Elegimos un punto O, llamado centro de semejanza, y la razón de semejanza k entre los dos polígonos. [...]
-
Si ABC y A9B9C9 son semejantes con razón de semejanza k, se cumple que: a9 = a · k, b9 = b · k, c9 = c · k y h9 = h · k. 7. [...]
-
La escala de un plano, mapa o maqueta es la razón de proporcionalidad entre las longitudes del objeto en la representación y las que le corresponden en la realidad. [...]
-
GeoGebra es un programa informático en línea que reúne dinámicamente aritmética, álgebra, geometría y cálculo. Ofrece para cada objeto matemático una Vista Algebraica y una Vista Gráfica. [...]
-
Anécdota de Tales de Mileto Aristóteles cuenta en su Política la siguiente anécdota de Tales: “Citaré lo que se refiere a Tales de Mileto, a propósito de una especulación lucrativa que le dio un crédito singular, honor debido sin duda a su ...
-
La aplicación de la proporcionalidad a la geometría conduce al concepto de semejanza entre figuras que se utiliza en la construcción de planos, mapas y maquetas, necesarios para poder representar la realidad en un tamaño manejable, interpretar...
-
La aplicación de la proporcionalidad a la geometría conduce al concepto de semejanza entre figuras que se utiliza en la construcción de planos, mapas y maquetas, necesarios para poder representar la realidad en un tamaño manejable, interpretar...
Cursos y asignaturas
-
Aún no hay comentarios, ¡comparte tu opinión! Inicia sesión o Únete a Tiching para poder comentar
La licencia digital es una autorización que permite utilizar un recurso digital de acuerdo con las condiciones legales de dicho recurso. El código que recibas una vez la hayas comprado te permitirá acceder al recurso educativo digital elegido.
Puedes consultar más información en nuestra página de ayuda.


























































































¿Dónde quieres compartirlo?
¿Quieres copiar el enlace?